Fraktály se hojně uplatňují v oboru počítačového výtvarného umění. Ve vhodném softwaru se fraktály bez většího úsilí samy vytvoří. Navíc fraktály pocházejí z obecné matematické formule, a tudíž nejsou zatíženy autorskými právy, jež by omezovala jejich další využití a publikaci. Umění spočívající v obarvování fraktálů z XaoSu názorně demonstruje například tato galerie.
Co jsou fraktály?
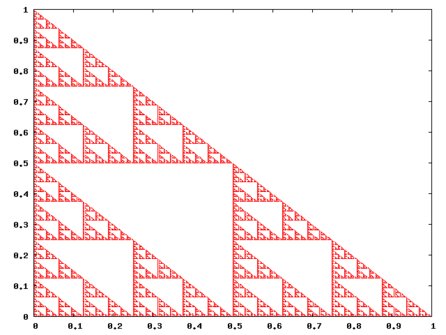
Zjednodušeně řečeno je fraktál vymezen jako množina v prostoru, pro niž jsou jednotlivé formální definice dimenze neekvivalentní. Pro podání základní představy využijme (deformovaného) Sierpińského trojúhelníku, jenž vidíte na obrázku.
Sierpińského trojúhelník
Tento útvar lze vygenerovat mnoha algoritmy:
-
Na obě souřadnice aplikuji bitový součet (operace
AND). Při nulovém výsledku patří bod do množiny. Tento algoritmus je implementačně nejjednodušší. -
Vezmu čtverec a „vyříznu“ pravý horní růžek tak, aby vznikly tři stejné poloviční čtverce. Postup stále opakuji.
-
Vezmu trojúhelník a z centra „vyříznu“ poloviční trojúhelník tak, že zbudou tři stejné trojúhelníky. Postup stále opakuji.
Z konstrukce plyne, že Sierpińského trojúhelník v sobě obsahuje své libovolně zmenšené kopie. Tato vlastnost je pro další výklad zásadní. Nechť pevně zvolený bod leží v některém z trojúhelníků. Pak musí ležet v jednom ze tří bezprostředně vnořených trojúhelníků. Informace o umístění bodu do jednoho z těchto tří trojúhelníků má velikost log(3) bitů. K snížení rozptylu o polovinu je tedy potřeba přibližně 1,585 bitu.
Úvaha jde zobecnit následujícím obvyklým způsobem. Maximální vzdálenost mezi body v kouli je rovna průměru koule. Vím-li, že bod leží v kouli o průměru r, pak znám polohu bodu s přesností r. Existuje-li pokrytí množiny n koulemi o poloměru r, pak k určení bodu s přesností r postačuje informace o velikosti log(n) bitů. Pokud minimální počet koulí potřebných k pokrytí množiny roste s x-tou mocninou převrácené hodnoty poloměru koulí, řekneme, že množina má dimenzi x.
Pro rozumné množiny (bod, kružnice, hyperbola, čtverec...) se výše vybudovaná definice kryje s intuitivní představou topologické dimenze. Pro Sierpińského trojúhelník je z předchozí úvahy zřejmé, že dimenze je log(3). Dimenze je tedy přibližně zmíněných 1,585, což nekoresponduje s intuitivní představou o celočíselném charakteru dimenze. V podobných situacích množinu nazýváme fraktálem.
Fraktály nejsou výhradně soběpodobné útvary. (Ačkoli někteří autoři zužují definici fraktálu jen na soběpodobné množiny.) Soběpodobnost Sierpińského trojúhelníku lze „zrušit“ například posunutím v ose x, které „zakřiví“ vertikální přímky. Křivost je totiž možné změřit a lze zpětně rekonstruovat měřítko, což vylučuje invariantnost vůči zvětšení.
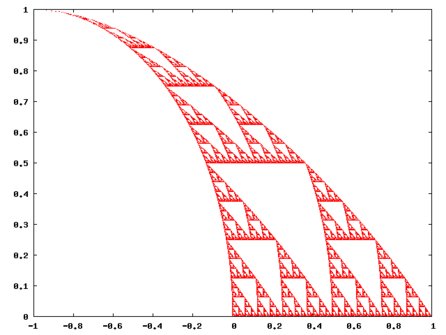Zakřivený Sierpińského trojúhelník
Další možností je například použití v pořadí druhého uvedeného algoritmu pro generování Sierpińského trojúhelníku. Jen místo pravého horního růžku vždy uřízneme náhodně jeden ze čtyř růžků. Možný výsledek vidíme níže. Čtenář si snadno zdůvodní, že uvedené transformace nezmění dimenzi. Výsledkem jsou tedy soběnepodobné fraktály.
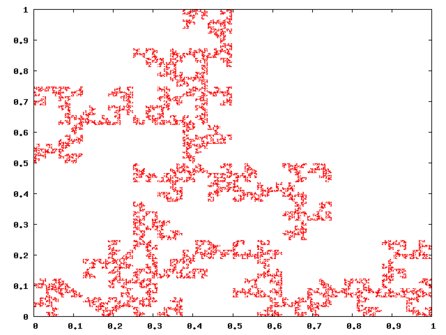Náhodně přeskupený Sierpińského trojúhelník
K vizualizace Sierpińského trojúhelníku nebyl použit XaoS, ale byla nasazena aplikace gnuplot způsobem popsaným v článku Gnuplot: Generujte grafy přímo z vašeho programu.
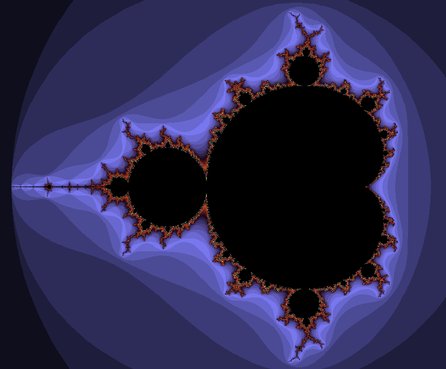
Aplikace XaoS obvykle nevytváří fraktály metodami vhodnými pro generování Sierpińského trojúhelníku. Místo toho opakovaně aplikuje nějaké zobrazení, které indukuje jevy studované v teorii chaosu. Potřebná zobrazení mohou být paradoxně velmi jednoduchá. Například Mandelbrotova množina vzniká následujícím postupem prováděným v aritmetice komplexních čísel.
-
Proměnná X se inicializuje nějakou hodnotou x, inicializuje se i konstanta C. Počet opakování se nastaví na nulu.
-
Proměnná X se umocní na druhou a přičte se k ní konstanta C. Odlišné transformace generují odlišné fraktály. Výsledek se uloží do X. Počet opakování se inkrementuje o jedničku.
-
Překročí-li absolutní hodnota X hodnotu 2, výpočet skončí.
-
Dosáhl-li počet opakování nastaveného maximálního počtu opakování, výpočet skončí.
-
Ve zbývajících případech se výpočet vrací zpět na druhý krok.
-
Bod je nakonec obarven podle dosaženého počtu opakování.
Výsledný program zobrazuje dvě komplexní hodnoty na jedno celé číslo. Definičním oborem je tedy čtyřrozměrný prostor. Počítačový monitor zobrazuje pochopitelně pouze dvojrozměrné podprostory. Ze všech možností, jak rozříznout čtyřrozměrný prostor rovinou, podporuje XaoS jen dva způsoby:
-
Proměnná x se zvolí pevně. Výsledkem je Mandelbrotova množina.
-
Proměnná C je zvolena pevně. Tedy souřadnice grafu jsou reálná a komplexní část hodnoty x. Tento graf se nazývá Juliova množina podle Gastona Julia, který se tématem zabýval na počátku dvacátého století.
Analogicky se v XaoSu konstruují i další fraktály a jejich Juliovy množiny.
Představení XaoSu
Jedná se o ryze jednoúčelový program s velmi triviálním uživatelským rozhraním. Proto se celý popis XaoSu zužuje na výčet jeho nejdůležitějších vlastností.
Základní vlastnosti XaoSu
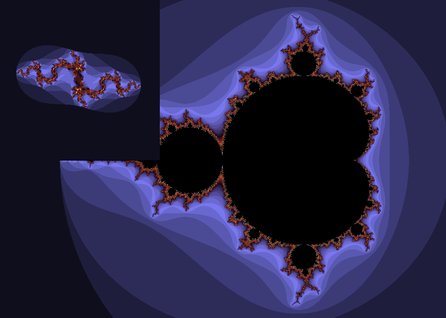
Vybraný fraktál můžete v XaoSu dynamicky a prakticky neomezeně zvětšovat v reálném čase. Levé tlačítko myši zvětšuje, pravé zmenšuje a prostřední umožňuje posouvat obraz. Vykreslování je optimalizováno pomocí unikátního algoritmu, který vyvinul český programátor Jan Hubička. XaoS proto pracuje velmi svižně.
Základní velikost
Zvětšení zesvětlené části
Zvětšení zesvětlené části
Zvětšení zesvětlené části
XaoS umí fraktály téměř libovolně zvětšovat a zmenšovat. Předcházející čtyři výřezy, které vznikly postupným zoomováním objektu pojmenovaného v XaoSu Phoenix. Přibližovaná místa jsou pro lepší orientaci označena zvýšeným jasem.
Mandelbrotova množina
V XaoSu jsou předdefinovány nejznámější fraktály. Na předchozím obrázku je vidět velmi známá Mandelbrotova množina.
Drobná chyba v definici Mandelbrotovy množiny
XaoS umí vykreslovat fraktály definované uživatelem zadanou formulí. Velmi složitá zadání však neúměrně přetíží počítač a zpomalí vykreslování. Předchozí výjev vznikl mírnou úpravou rovnice definující Mandelbrotovu množinu.
Základní obarvení
Náhodné obarvení
Náhodné obarvení
XaoS umí fraktál náhodně obarvit. Uživatel si také může přesně nastavit požadované obarvení.
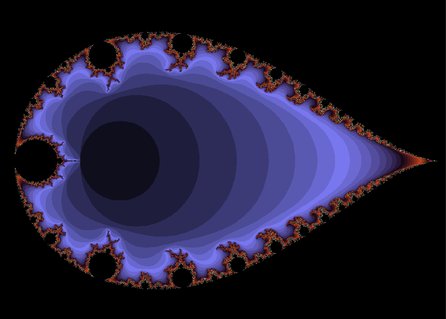Transformovaná Mandelbrotova množina
XaoS umí provést základní planární transformace. Není proto nutné tyto změny emulovat změnami v definičních formulích. Na ukázku zde byla vykreslena kruhová inverze Mandelbrotovy množiny.
Filtr detekce hran
XaoS umí na obrázek aplikovat grafické filtry, takže není potřeba využívat GIMP nebo jiné externí bitmapové grafické editory.
Juliova množina
K libovolnému bodu si lze ve vnořeném okně nechat vykreslit odpovídající Juliovu množinu.
Další vlastnosti XaoSu
-
Program je uvolněn pod svobodnou licencí GNU GPL.
-
Prostředí je téměř kompletně přeloženo do češtiny.
-
Práce v XaoSu nevyžaduje hlubší porozumění matematické podstatě generování fraktálů.
-
Lze nastavit počet iterací a další parametry výpočtu.
-
XaoS umí sejmout obrazovku a uložit obrázek. Počítá se i s nahráváním videa.
-
XaoS nabízí velmi pěkný animovaný tutoriál.
-
XaoS ukládá historii uživatelských akcí. Nežádoucí změny se dají vracet.
Předpřipravené fraktály
V XaoSu je předdefinováno několik fraktálů:
Mandelbrotova množina a fraktál Phoenix již byly zmíněny. Jejich znázornění naleznete výše.
Mandelbrotova množina definovaná s pátou mocninu
V definiční formuli Mandelbrotovy množiny lze použít vyšší mocniny. Zobrazenou Mandelbrotovu množinu vytváří místo druhé pátá mocnina.
Fraktál Newton
Fraktál v XaoSu pojmenovaný jako Newton vychází z metody hledání řešení Newtonovou metodou sečen. Tři pravidelně rozmístěné rozlehlé oválné „skvrny“ jsou okolími jednotlivých kořenů rovnice.
Newton definovaný s pátou mocninou
Podobně jako u Mandelbrotovy množiny nechybí ani u Newtonu řešení pro polynomy vyšších stupňů.
Fraktál Barnsley
Fraktály Barnsley objevil Michael Barnsley, který studoval nasazení fraktálů při kompresi obrázků. Bližší informace jsem nezjistil.
Fraktál Magnet
Fraktály Magnet a Magnet 2 rovněž nejsou dokumentovány. Pravděpodobně se jedná o řešení uspořádání magnetických domén v materiálu za kritických podmínek odpovídajících fázovému přechodu.
Podobný software
Elementárními schopnostmi v oblasti fraktální grafiky disponuje velký počet programů. Například GIMP funkcí „badatel fraktálů“ počítá několik fraktálů a zobrazuje jejich předem vybrané zajímavé výřezy. Vybraný fraktál označovaný „Ledový krystal“ vygenerovaný GIMPem je ve skutečnosti částí z Mandelbrotovy množiny.
Výstup badatele fraktálů z GIMPu
Dále existují specializované programy zaměřené přímo na fraktály. Uveďme třeba Electric sheep. Přímý konkurent XaoSu však pravděpodobně neexistuje.
